반응형

백준 3344 N-Queen
https://www.acmicpc.net/problem/3344
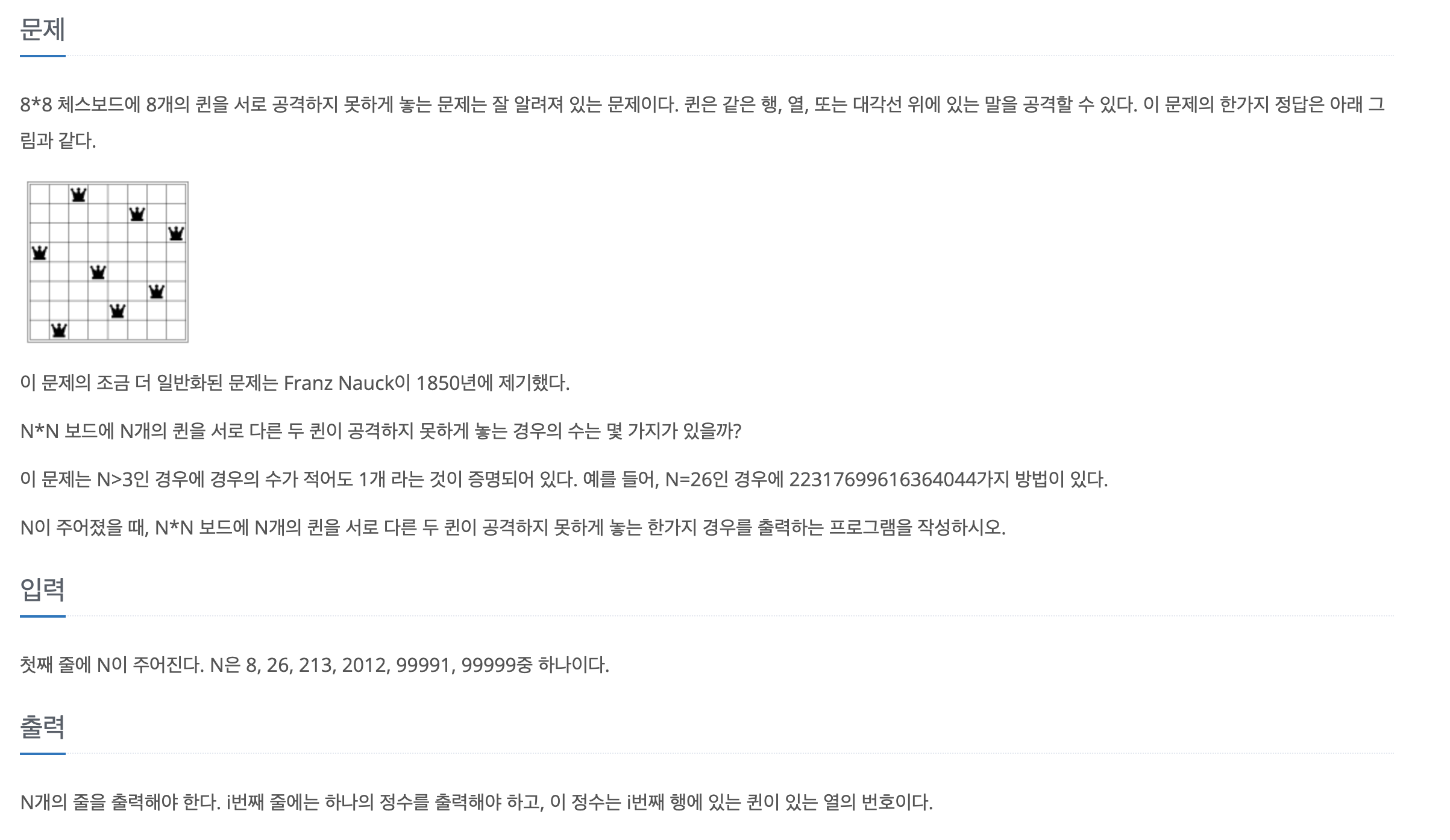
시도 1 : 백트래킹 (실패)
백트래킹 예제 풀다가 변형해서 제출했는데 N 최대가 99999라서 시간 초과가나온다.
N = int(input())
ans = []
for i in range(0, N):
ans.append(-1)
def queen(num):
if check(num) == True:
if num == N:
for a in ans:
print(a+1)
exit(0)
else:
for j in range(0, N):
ans[num] = j
queen(num+1)
def check(num):
for k in range(0, num-1):
if ans[num-1] == ans[k]:
return False
elif abs(ans[num-1] - ans[k]) == (num-1-k):
return False
return True
queen(0)
풀이
풀이 1
위키피디아에 N-Queen 문제 접근법이 나온다.
N이 8이상이면 규칙이 있는데, N을 나눈 나머지가 2냐, 3이냐, 기타냐 에 따라 달라진다.
1. If the remainder from dividing n by 6 is not 2 or 3 then the list is simply all even numbers followed by all odd numbers not greater than n.
2. Otherwise, write separate lists of even and odd numbers (2, 4, 6, 8 – 1, 3, 5, 7).
3. If the remainder is 2, swap 1 and 3 in odd list and move 5 to the end (3, 1, 7, 5).
4. If the remainder is 3, move 2 to the end of even list and 1,3 to the end of odd list (4, 6, 8, 2 – 5, 7, 9, 1, 3).
5. Append odd list to the even list and place queens in the rows given by these numbers, from left to right (a2, b4, c6, d8, e3, f1, g7, h5).
For n = 8 this results in fundamental solution 1 above.
A few more examples follow.
14 queens (remainder 2): 2, 4, 6, 8, 10, 12, 14, 3, 1, 7, 9, 11, 13, 5.
15 queens (remainder 3): 4, 6, 8, 10, 12, 14, 2, 5, 7, 9, 11, 13, 15, 1, 3.
20 queens (remainder 2): 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 3, 1, 7, 9, 11, 13, 15, 17, 19, 5.
구현
odd, even 리스트를 만들어서 나머지가 2, 3인 경우 순서를 바꿔주고 even + odd 를 출력하면 된다.
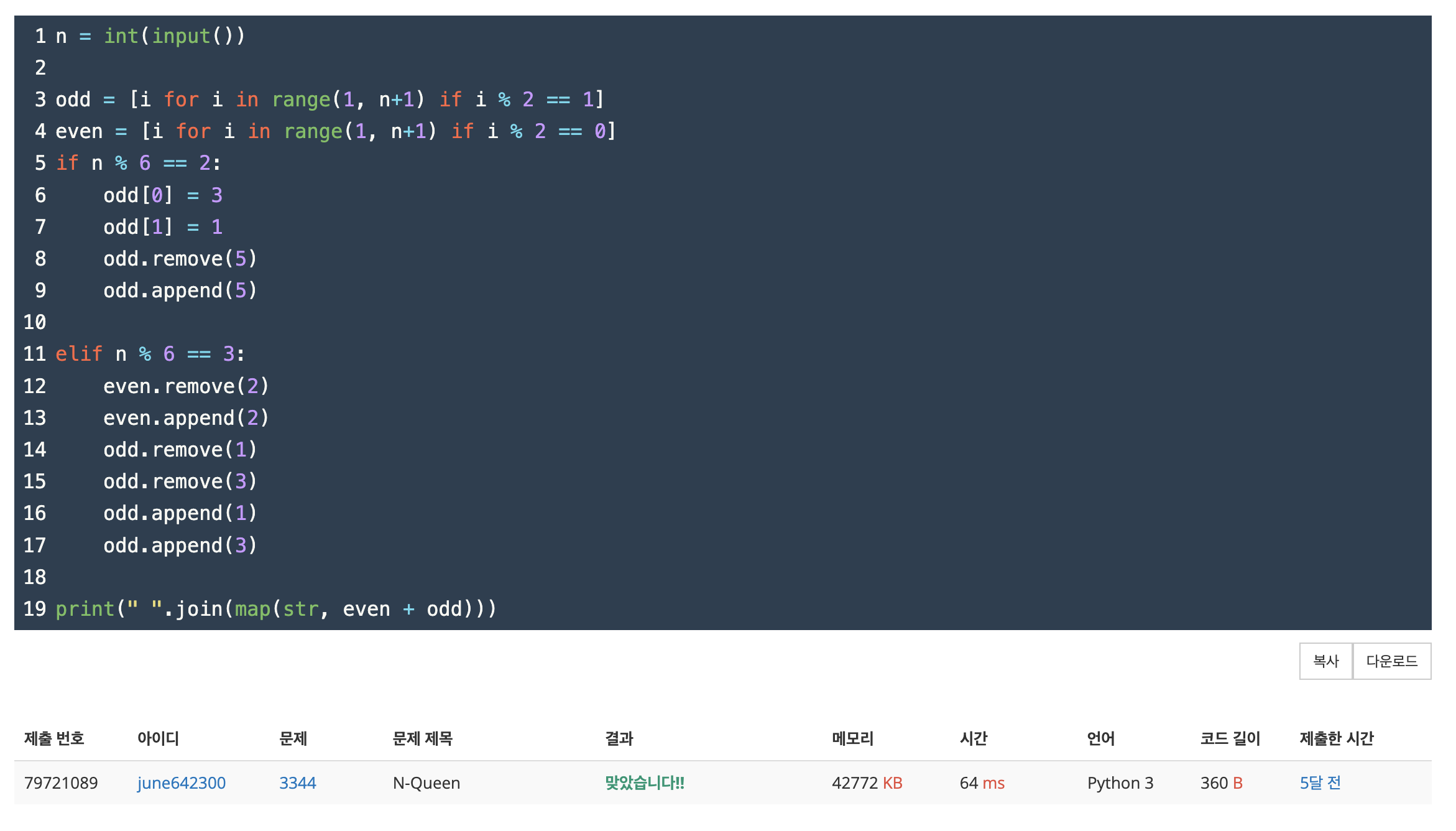
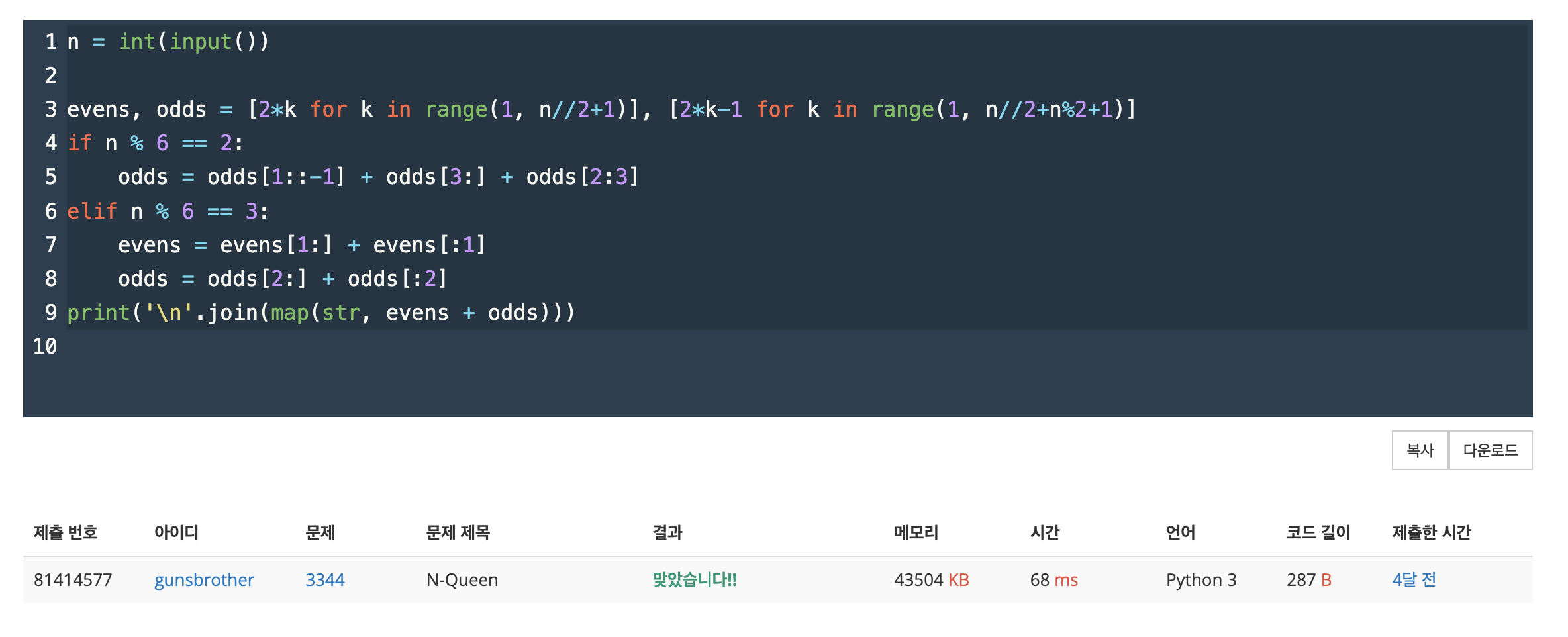
풀이 2
컴퓨터 과학자 Niklaus Wirth 의 풀이를 python으로 바꾼 코드이다.
리스트를 사용하지 않고 제너레이터 형태로 코루틴을 사용했다.
def queens(n: int, i: int, a: list, b: list, c: list):
if i < n:
for j in range(n):
if j not in a and i + j not in b and i - j not in c:
yield from queens(n, i + 1, a + [j], b + [i + j], c + [i - j])
else:
yield a
for solution in queens(8, 0, [], [], []):
print(solution)풀이 3
geeksforgeeks 에 백트래킹으로 푼 N-Queen 문제 풀이
메모리 초과난다.
# Python3 program to solve N Queen Problem using
# backtracking
N = 4
# ld is an array where its indices indicate row-col+N-1
# (N-1) is for shifting the difference to store negative
# indices
ld = [0] * 30
# rd is an array where its indices indicate row+col
# and used to check whether a queen can be placed on
# right diagonal or not
rd = [0] * 30
# Column array where its indices indicates column and
# used to check whether a queen can be placed in that
# row or not
cl = [0] * 30
# A utility function to print solution
def printSolution(board):
for i in range(N):
for j in range(N):
print(board[i][j], end=" ")
print()
# A recursive utility function to solve N
# Queen problem
def solveNQUtil(board, col):
# Base case: If all queens are placed
# then return True
if (col >= N):
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range(N):
# Check if the queen can be placed on board[i][col]
# To check if a queen can be placed on
# board[row][col] We just need to check
# ld[row-col+n-1] and rd[row+coln]
# where ld and rd are for left and
# right diagonal respectively
if ((ld[i - col + N - 1] != 1 and
rd[i + col] != 1) and cl[i] != 1):
# Place this queen in board[i][col]
board[i][col] = 1
ld[i - col + N - 1] = rd[i + col] = cl[i] = 1
# Recur to place rest of the queens
if (solveNQUtil(board, col + 1)):
return True
# If placing queen in board[i][col]
# doesn't lead to a solution,
# then remove queen from board[i][col]
board[i][col] = 0 # BACKTRACK
ld[i - col + N - 1] = rd[i + col] = cl[i] = 0
# If the queen cannot be placed in
# any row in this column col then return False
return False
# This function solves the N Queen problem using
# Backtracking. It mainly uses solveNQUtil() to
# solve the problem. It returns False if queens
# cannot be placed, otherwise, return True and
# prints placement of queens in the form of 1s.
# Please note that there may be more than one
# solutions, this function prints one of the
# feasible solutions.
def solveNQ():
board = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
if (solveNQUtil(board, 0) == False):
printf("Solution does not exist")
return False
printSolution(board)
return True
# Driver Code
if __name__ == '__main__':
solveNQ()
# This code is contributed by SHUBHAMSINGH10
참고
728x90
반응형
'개발 > Algorithm 문제 풀이' 카테고리의 다른 글
| [프로그래머스] lv.1 개인정보 수집 유효기간 (0) | 2024.02.12 |
|---|---|
| [프로그래머스] lv2. 순위 검색 (0) | 2024.02.12 |
| [프로그래머스] lv.1 가장 많이 받은 선물 (0) | 2024.01.29 |
| [프로그래머스] lv.2 과제 진행하기 (0) | 2024.01.28 |
| [프로그래머스] for 문과 if문을 한번에 (0) | 2022.07.15 |


